个人简介
小公司研发总监,既当司令也当兵!
文章分类
相关博文
- ·
- ·
- ·
- ·
- ·
- ·
- ·
- ·
- ·
- ·
分类: linux
2016-02-16 22:15:00
二叉堆的定义
二叉堆是完全二叉树或者是近似完全二叉树。
二叉堆满足二个特性:
1.父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆:
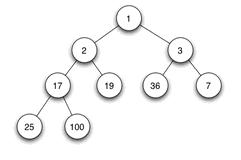
由于其它几种堆(二项式堆,斐波纳契堆等)用的较少,一般将二叉堆就简称为堆。
堆的操作一般包括初始化、插入和删除:
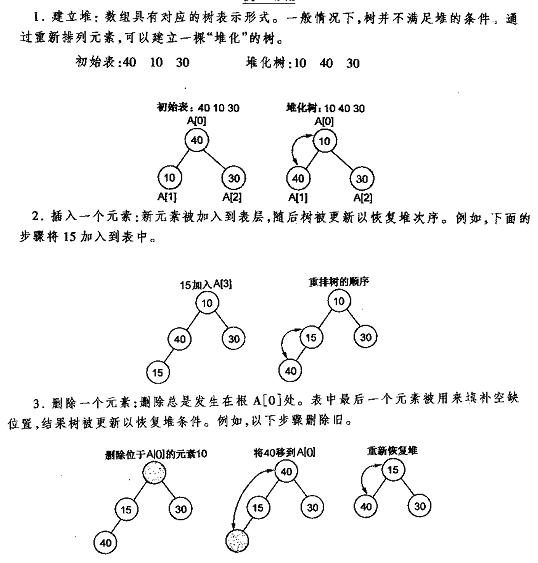
下面是堆的简单实现:
点击(此处)折叠或打开
-
typedef struct struct_heap {
-
-
int size;
-
int head;
-
int *data;
-
}heap_t;
-
-
void initheap(heap_t **heap, int size)
-
{
-
heap_t *pheap;
-
-
pheap = (heap_t*)malloc(sizeof(*pheap) size * sizeof(int));
-
if (null == pheap)
-
{
-
printf("malloc fail\n");
-
return;
-
}
-
memset(pheap, 0, sizeof(*pheap) size * sizeof(int));
-
-
pheap->size = size;
-
pheap->head = 0;
-
pheap->data = (int *) ((char *)pheap sizeof(*pheap));
-
-
*heap = pheap;
-
}
-
-
void insertheap(heap_t *pheap, int key)
-
{
-
int cursor;
-
int tmp;
-
-
if (null == pheap)
-
return;
-
-
if (pheap->head == pheap->size)
-
{
-
printf("heap is full\n");
-
return;
-
}
-
-
pheap->data[pheap->head] = key;
-
-
cursor = pheap->head - 1;
-
-
while (cursor > 0)
-
{
-
if (pheap->data[cursor] < pheap->data[(cursor - 1)/2])
-
{
-
tmp = pheap->data[cursor];
-
pheap->data[cursor] = pheap->data[(cursor-1) /2];
-
pheap->data[(cursor-1) / 2] = tmp;
-
cursor = (cursor - 1) / 2;
-
}
-
else
-
break;
-
}
-
}
-
-
void deleteheap(heap_t *pheap, int *out)
-
{
-
int cursor;
-
int temp;
-
int left;
-
int right;
-
int key;
-
-
if (null == pheap)
-
return;
-
-
if (pheap->head == 0)
-
{
-
printf("heap is empty\n");
-
return;
-
}
-
-
*out = pheap->data[0];
-
pheap->data[0] = pheap->data[pheap->head - 1];
-
pheap->head--;
-
-
cursor = 0;
-
while (cursor < pheap->head -1)
-
{
-
key = pheap->data[cursor];
-
left = key < 0 ? (key * -2) : (key * 2 1);
-
right = left 1;
-
-
if ( (2 * cursor 1) <= pheap->head -1)
-
{
-
left = pheap->data[2*cursor 1];
-
}
-
if ( (2 * cursor 2) <= pheap->head -1)
-
{
-
right = pheap->data[2*cursor 2];
-
}
-
-
if (key > left && left < right)
-
{
-
temp = pheap->data[cursor];
-
pheap->data[cursor] = pheap->data[2 * cursor 1];
-
pheap->data[2 * cursor 1] = temp;
-
cursor = 2 * cursor 1;
-
}
-
else if (key > right && right < left)
-
{
-
temp = pheap->data[cursor];
-
pheap->data[cursor] = pheap->data[2 * cursor 2];
-
pheap->data[2 * cursor 2] = temp;
-
cursor = 2 * cursor 2;
-
}
-
else
-
break;
-
}
- }
堆排序
理解堆的插入和删除后,堆排序实现就非常简单了。下面是堆排序的简单实现:
点击(此处)折叠或打开
-
// 在index位置插入新元素后,修正堆序列使之满足堆要求
-
static void minheapfixup(int list[], int index)
-
{
-
int cursor;
-
int temp;
-
-
cursor = index;
-
while (cursor > 0)
-
{
-
if (list[cursor] < list[(cursor -1)/2])
-
{
-
temp = list[cursor];
-
list[cursor] = list[(cursor-1)/2];
-
list[(cursor-1)/2] = temp;
-
cursor = (cursor - 1) / 2;
-
}
-
else
-
break;
-
}
-
}
-
-
// 删除堆顶元素后,将最后一个元素移至堆顶,修正堆序列使之满足堆要求
-
static void minheapfixdown(int list[], int len)
-
{
-
int cursor;
-
int temp;
-
-
int key;
-
int left;
-
int right;
-
-
cursor = 0;
-
-
while (cursor < len)
-
{
-
key = list[cursor];
-
-
if ( 2 * cursor 1 < len)
-
left = list[2 * cursor 1];
-
else
-
left = key 1;
-
-
if ( 2 * cursor 2 < len)
-
right = list[2 * cursor 2];
-
else
-
right = key 2;
-
-
if (key > left && left < right)
-
{
-
temp = key;
-
list[cursor] = left;
-
list[cursor * 2 1] = temp;
-
cursor = cursor * 2 1;
-
}
-
else if (key > right && right < left)
-
{
-
temp = key;
-
list[cursor] = right;
-
list[cursor * 2 2] = temp;
-
cursor = cursor * 2 2;
-
}
-
else
-
break;
-
}
-
}
-
-
void heapsort(int list[], int len)
-
{
-
int i;
-
int temp;
-
-
for (i = 1; i < len; i)
-
minheapfixup(list, i);
-
-
for (i = len; i > 1; i--)
-
{
-
temp = list[0];
-
list[0] = list[i - 1];
-
list[i - 1] = temp;
-
-
minheapfixdown(list, i - 1);
-
}
- }
给主人留下些什么吧!~~